| Everyday Math Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 5 |
|
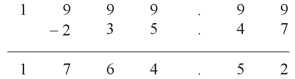
1. We've borrowed improperly in the rightmost column. Instead of ending up with 9 in the topmost row (small digits), we should have written down 10. We also forgot to borrow in the leftmost column, deleting the 1 to get 0, which we don't have to write down in the topmost small row because it's in the leftmost column (so in effect, it vanishes). The correct choice is B. We made two borrowing mistakes, one in the far left column and one in the far right column. When we do the problem correctly, we get the matrix shown below.
|
|
2. In this situation, we don't have to borrow at all! We've made the problem a lot harder than it really is, committing errors in every single column except the one at the far left. The answer is C. When we do the problem correctly, we obtain the following array of digits, without any borrowing operations whatsoever.
|
|
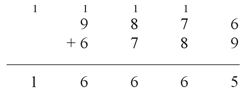
3. We've forgotten to carry digits in the addition matrix, producing an incorrect sum. Here's what the array (with the correct sum) should look like:
The carried digits are the small numerals 1 in the very top row. In the book text, this row is entirely missing. The correct choice is B. |
|
4. We've made a mistake in one of the single-digit multiplication steps. We multiplied 8 by 3 and wrote it down as 27, when it actually equals 24! Here's the corrected matrix:
In the row that said 1878 in the original statement of the question, we now write the numeral 1848. In the second column from the right, we add the 4 in 1848 to the 2 in 4620 to get 6, so our final answer becomes 6468 rather than 6498. The original statement didn't contain any errors other than the single multiplication mistake described above, so the answer is A. |
| 5. If we reverse the order of a subtraction problem, we end up with the negative (or additive inverse) of the result that we got before. For example, 7 - 2 = 5, but 2 - 7 = -5. The correct choice is B. |
|
6. We've made a subtle mistake in one of the single-digit multiplication steps here. Instead of multiplying the 6 in 306 by the 0 in 108 to get 0 and then adding the carried digit 4, we multiplied the 6 in 306 by the carried digit 4 itself, getting 24! From there, the problem continued on using some mistaken values. Here's the corrected matrix:
In the row that said 848 in the original statement of the question, we now have 648. We lose the improperly carried digit 2 that appeared above the 1 in 108. These corrections cause the center digit in our final answer to change from 2 to 0. We didn't make any other mistakes in the execution of this problem, besides the inadvertent mistreatment of the carried 4 and the improperly carried digit 2. The correct choice is therefore A. |
| 7. This longhand addition problem contains no errors or formatting inconsistencies. We've done it perfectly. The answer is D. |
| 8. This longhand division problem contains no errors or formatting inconsistencies. We've done it perfectly. The answer is D. |
| 9. If we reverse the order of the quantities in a division problem, we end up with the reciprocal (or multiplicative inverse) of the result that we got before, as long as neither of the values equal 0. For example, 150/30 = 5, but 30/150 = 1/5. The correct choice is C. (If either value equals 0, we end up dividing by 0 either in the original quotient, or in the transposed quotient. Remember, mathematicians do not define division by 0 at all; it's simply forbidden!) |
|
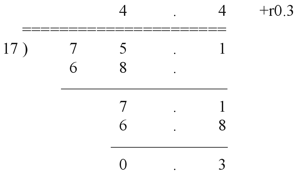
10. We've committed an internal multiplication error. When we multiplied the first number 4 (immediately to the left of the decimal point in the answer row) by 17 (the divisor), we should have written down 68 underneath the digits 75 (the whole-number part of the dividend). From that point onward, the results in the corrected problem differ from those shown in the statement of the question. Here's the matrix as it should appear:
The original statement didn't contain any errors other than the single multiplication mistake described above (even though that single error propagated through the rest of the problem). The answer is A. |