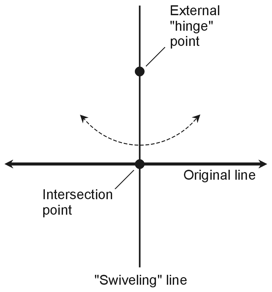
4. According to the Perpendicular Principle, if you have a straight line and a point that doesn't lie on that line, you can draw one and only one (or exactly one) line through the point and also through the original line, such that the new line runs perpendicular to the original line. The drawing below (based on Figure 1-5 on page 10 of the book text) shows the situation.

Imagine "swiveling" the new line on the external point, as if that point is a hinge, all the while making sure that the two lines intersect. You can see that one, but only one, position of the new line will give you a right angle where the two lines intersect. The correct choice is B.

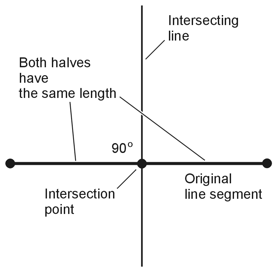
5. The Perpendicular Bisector Principle says that if you have a straight line segment and a line crosses through it at a right angle (90º), then you can find one and only one (or exactly one) place where the crossing line can lie so that it divides the original line segment into two equal parts. The drawing below shows the situation. (It's a modified version of Figure 1-6 on page 10 of the text.)

Imagine that you move the vertical intersecting line to the left and right, all the while keeping it perpendicular to the original line segment. You'll only be able to make the intersecting line bisect (cut in half) the original line segment in one location. The correct choice is B.

6. Let's go through all the choices, one by one. That way, we can arrive at our answer by elimination.

• Choice A: Angles w and s constitute corresponding angles, which always have equal measure in a situation such as the one shown in Figure 1-15. This isn't the choice we want!
• Choice B: Angles w and u are alternate exterior angles, which always have equal measure in a situation like that of Figure 1-15. This choice won't work!
• Choice C: Angles v and y have nothing special to distinguish them. In fact, we can easily see, just by examining Figure 1-15, that these two angles can differ in measure. Apparently, this is the correct choice. But let's look at D to make certain.
• Choice D: Angles v and z are corresponding angles. They always have equal measure in situations like the one in Figure 1-15.

The answer is C, sure enough!

7. Let's "adjust" the transversal line in Figure 1-15 so that angles s and v have equal measure. We know that the measures of s and v must add up to 180º because they're adjacent angles, and adjacent angles always sum to a straight angle (180º). We've deliberately made s = v, so we know that s + v = 180º and s = v. Simple algebra tells us that s = 90º and v = 90º in this case, so the transversal must run perpendicular to the bottom horizontal line. We can also see that s and w are corresponding angles, so we can conclude that w = s = 90º. Similarly, v and z are corresponding angles, so z = v = 90º. Because w and z are adjacent angles and both have measures of 90º, it follows that the transversal must run perpendicular to the top horizontal line. Having shown that the transversal runs perpendicular to both parallel lines, we must choose A as our answer.

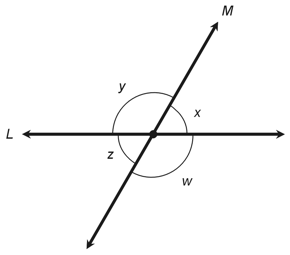
8. When you have two intersecting straight lines, you get four angles, and four pairs of adjacent angles. The following illustration shows an example.

Let's call the two intersecting lines L and M and name the four angles w, x, y, and z. You can identify four adjacent-angle pairs, as follows:

• Angles w and x
• Angles x and y
• Angles y and z
• Angles z and w

In any case, when you add the measures of a pair of adjacent angles, you'll get a straight angle. The measure of a straight angle equals 180º (or π radians) by definition. When you let your gaze rotate counterclockwise through each pair of adjacent angles, you'll see that in every case, the pair adds up to an angle whose sides both lie along line L, or else both lie along line M. Those four "sum angles" all constitute straight angles at the intersection point between lines L and M. The correct choice is B.