| Geometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 3 |
|
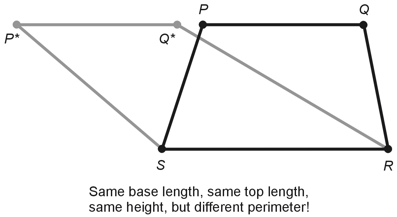
1. If we know the length of the top, the length of the base, and the height of a trapezoid, we still don't have enough information to determine the perimeter. Consider a variant P*Q*RS of trapezoid PQRS (from Figure 3-18 on page 66 of the book text), as shown below.
Suppose that the length of line segment P*Q* equals the length of line segment PQ. Also suppose that both of these line segments lie along the same line. In this case, trapezoids P*Q*RS and PQRS have the same top length (7 units), the same base length (9 units), and the same height (6 units), but we can easily see that the perimeter of P*Q*RS exceeds the perimeter of PQRS. The correct choice is D. If we "morph" the trapezoid by moving the top side to the right or the left by a great enough distance while keeping the top length the same, the base length the same, and the height the same, we can make the perimeter larger and larger without limit. |
| 2. To find the interior area of a trapezoid, we average the top length and the base length, and then multiply by the height. In the scenario of Figure 3-18, the top measures 7 units long and the base measures 9 units long, so the average equals 8 units. The height equals 6 units. Therefore, the area equals 8 x 6, or 48, units squared. The answer is B. Interestingly, we can "morph" the trapezoid by moving the top back and forth (an example of which appears in the drawing for the solution to Question 1, above), and as long as we keep the top length the same, and as long as we make sure that the top of the "morphed" trapezoid stays in line with the top of the original one, the area will never change. This curious fact remains true even if we move the top to the left or right by 10 units, or 100 units, or 1,000,000 units! |
| 3. In Figure 3-18, triangle SQR has a base length of 9 units and a height of 6 units. Recall that the area of a triangle equals half the product of the base length and the height. Triangle SQR therefore has an interior area of (1/2) x 9 x 6, or 27, units squared. The correct choice is A. |
| 4. Let's call line segment PQ the "base" of triangle PQS. (The triangle thus appears "upside down.") The base length is 7 units. The height is 6 units. The area therefore equals (1/2) x 7 x 6, or 21, units squared. The answer is C. |
| 5. A square is a rhombus with interior angles all measuring 90º. A square is a parallelogram whose interior angles all measure 90º, and whose sides all have the same length. A square constitutes a rectangle whose sides all have the same length. All three choices A, B, and C produce true statements when we complete the question's sentence with them, so the answer is D, "All of the above." |
| 6. If the angle x in Figure 3-19 measures π/2 rad (a right angle), then we know that the object PQRS constitutes a rhombus, so all four sides have equal lengths. The correct choice is A. |
| 7. If we want to calculate the interior area of a rectangle, we multiply its base length by its height. We can, in effect, accomplish that task by finding the product of the lengths of any two adjacent sides: the base and the left-hand side, the left-hand side and the top, the top and the right-hand side, or the right-hand side and the base. This scheme works only because all four interior angles are right angles, so the left-hand and right-hand sides define the rectangle's height. The correct choice is A. |
| 8. The sum of the measures of the interior angles in any quadrilateral, including a trapezoid, equals 2π rad (a full circle or 360º). The correct choice is C. |
|
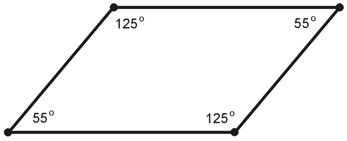
9. In a parallelogram, opposite interior angles have equal measure, and the measures of all four interior angles add up to 2π rad or 360º. Those are the only two requirements for a quadrilateral to "qualify" as a parallelogram. We can find plenty of parallelograms for which none of the choices A, B, or C will produce valid statements. Consider the specific example shown below. One pair of opposite interior angles adds up to 125º + 125º = 250º, while the other pair adds up to 55º + 55º = 110º. The measures of all four interior angles sum up to 2π rad or 360º, as they must in any quadrilateral.
Neither pair of opposite interior angles adds up to a straight angle (π rad or 180º), a complete circle (2π rad or 360º,), or a right angle (π/2 rad or 90º). None of the choices A, B, or C will work for this particular parallelogram. We can't have complete confidence in any of them in the general case. The answer is D, "None of the above." |
|
10. An interior angle in a plane quadrilateral must always have positive measure (greater than 0 rad or 0º), but must remain less than a full circle (2π rad or 360º). If we call such an angle x, then we can express the foregoing constraint as 0 rad < x < 2π rad The correct choice is B. |