| Geometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 4 |
|
1. In order to solve this problem, we'll need the formula for the individual interior angles of a regular polygon. That formula appears on page 76 of the text. If we have a regular polygon with n sides, we can calculate the measure θ of each interior angle, in radians, as follows: θ = (πn - 2π) / n In this case n = 7, so θ =
(7π - 2π) / 7 The answer is B. |
| 2. In a regular plane polygon, all interior angles have the same measure. As the number of sides increases, the measure of each interior angle also increases, but that measure can never reach or exceed the measure of a straight angle (π rad or 180º). The correct choice is B. |
| 3. In a general plane polygon (whether regular or not), an interior angle can never reach or exceed the equivalent of a full circular rotation. That's 2π rad or 360º. The answer is D. |
| 4. As we indefinitely increase the number of sides in a regular plane polygon, the measure of each interior angle approaches π rad or 180º. The number of interior angles increases right along with the number of sides. Therefore, as the number of sides in a regular polygon "approaches infinity" (that's an alternative way to say "increases without limit"), the sum of the measures of all the interior angles "approaches 180º times infinity." From this observation, we can see that no limit exists as to how large the angle-measure sum can get. The correct choice is C. |
|
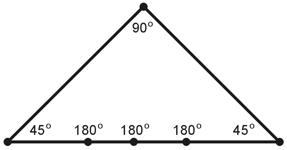
5. In a plane polygon, three vertices can lie along a single line; it simply means that the figure must have at least four vertices, and at least one interior angle must measure π rad or 180º. See the drawing below for an example. It's a hexagon with three straight angles. (We get a "bonus" here, because not only three, but five, vertices lie along the same straight line!) We can rule out choice A.
For a geometric figure to constitute a true plane polygon, all of the vertices must lie in a single plane, so we can rule out choice B. In any plane polygon, each and every side must be a line segment of nonzero, finite length, so we can rule out choice C. By elimination, only choice D remains as an option! When we scrutinize it, we can see that it's indeed the right answer. In a "legal" plane polygon, no two sides can cross over each other. |
| 6. To calculate the area of an ellipse, we multiply π times the length of the major semiaxis times the length of the minor semiaxis. In this case, that product is 3.14159 x 8 x 6, or 150.796 square units, rounded off to three decimal places. (We've been told to assume that the values 8 and 6 are mathematically exact.) The correct choice is B. |
|
7. To calculate the approximate circumference of an ellipse, we must go through several steps, as shown in the formula on page 81 of the text. First, we must square the lengths of the semiaxes. When we do that, we get 82 = 64 and 62 = 36. Next, we add, getting 64 + 36 = 100. Then we divide by 2, getting 50. (So far, all these values are mathematically exact.) Now we must take the square root of 50. A calculator tells us that it's approximately 7.07107. Finally we must multiply by 2π, which equals approximately 6.28318. Once again using our trusty calculator, we get 7.07107 x 6.28318 = 44.4 units, rounded off to the nearest tenth of a unit (one decimal place). The answer is D. |
|
8. To calculate the interior area of a circle, we must square the radius and then multiply by π. If we call the interior area A, then A = πr2 for the entire circle. In this case, we get A = π x 42 We want to figure out the area of the sector outlined with the heavy solid lines and curves. Figure 4-15 on page 89 tells us that the sector spans 2 rad. That's 2/(2π), or 1/π of the full circle. We've determined that the circle has an area of 16π square units. When we multiply this quantity by 1/π, we get the area of the circular sector (let's call it A*), as follows: A* = 16π x (1/π) The answer is C. |
| 9. First, let's figure out the arc length of the circular part of the sector's outline. Then we can simply add twice the radius to that quantity to get the perimeter of the sector. The arc spans an angle of 2 rad, while a full circle spans 2π rad. Therefore, the arc length must equal 2/(2π), or 1/π, of the whole circle's circumference. That circumference equals 2 times π times the radius, or 2 x π x 4, which is 8π. The arc length is 1/π of this quantity, or 8 units. We can see that the radius equals 4 units and we must go twice through that radius to get around the sector. The perimeter of the sector therefore equals 4 + 4 + 8, or 16 units. The correct choice is C. |
| 10. When we solved Question 8, we determined that in Figure 4-15, the area of the bold-outlined circular sector equals 1/π of the entire circle's area. The answer is A. |