Geometry Demystified, 2nd edition

Stan Gibilisco

Explanations for Quiz Answers in Chapter 5

1. If you want to "record" a distance such as the length of a line segment or the separation between two points, you may not use any device with calibration marks (such as a ruler), or make marks on anything except the page on which you're performing the construction. Choice A won't work. Choice B doesn't provide any particular reference distance. It says nothing about the actual radii of the circles that you might draw. Therefore, choice B is wrong. You can take advantage of the fact that when you set the pencil tip and the nonmarking tip of a compass a certain distance apart, it "establishes" that distance. Choice C will do the job here, so it's the correct answer.

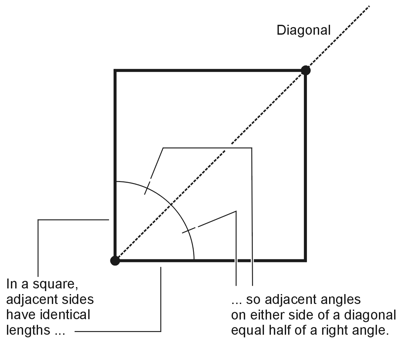
2. A 45º angle has half the measure of a 90º (right) angle. Therefore, if we can manage to bisect a right angle (an easy enough construction to do), we'll get a 45º angle (two of them, actually). All of the three choices A, B, and C describe ways to bisect a right angle. As for the right angles available for bisection:

All of the interior angles of a square are right angles. When we draw a diagonal to a square, we "automatically" bisect the right angle at either end of the diagonal because, in a square, any two adjacent sides have identical lengths (see the drawing below). This fact accounts for choice A. (We haven't proven it, but if you like, you can demonstrate it as an "extra-credit" exercise.)
When we construct the perpendicular bisector of a line segment, we "automatically" construct four right angles. This fact takes care of choice B.
All of the interior angles of a rectangle are right angles. This fact accounts for choice C.

The correct response to this question is D, "Any of the above."

3. We must complete a geometric construction entirely in the real world, with a limited selection of physical objects (compass, straight edge, pencil, and paper only). We can imagine what might happen if we could bisect an angle infinitely many times, or reproduce a line segment infinitely many times, but we can't physically do those things. We're allowed to reproduce angles (so choice A is wrong); we aren't confined to lines and points only (so choice B is wrong); we aren't allowed to use a drafting triangle at all (so choice D is wrong). However, in real life, we must always finish the job in a finite amount of time, and we have to do it in a physical way (not merely in our minds.) It follows that we must complete the construction in a finite number of steps. The correct choice is C.

4. No instrument meant to perform geometric constructions can "legally" have any sort of calibrated scale, so we can rule out choice B. A compass can draw circles but not ellipses, so we can rule out choice C. A compass has only one pencil, so we can rule out choice D. The only remaining choice is A, and it's the correct answer: A compass intended for geometric constructions must lack a scale for measuring angles (or if it has one, we must not look at it!).

5. If we want to construct a line segment whose length exceeds the length of our straight edge, we should find a longer straight edge so that we can construct the desired line segment in a "single swipe." The correct choice is B.

6. If we want to construct a circle with half the radius of a specific circle whose center point we've located, we must physically define the radius of the existing circle by drawing a line segment from the circle's center point outward (in any direction) until it passes through the circle. (In order to do that, we have to know the exact location of the circle's center. Problem 5-1 on page 98 presupposes that knowledge, because it instructs us to create the original circle on the basis of a chosen center.) We can then bisect the portion of the line segment whose end points lie at the center of the circle and on the circle itself. Once we've bisected that line segment (and thereby bisected the original circle's radius), we can set our compass to a span equal to either half of the bisected line segment. Finally we can draw a new circle whose radius equals the compass span. The correct choice is A.

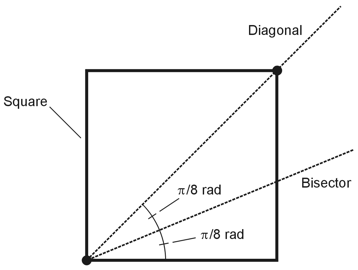
7. We've established the fact that when we draw a diagonal across a square, we get two adjacent angles that have equal measures, both equivalent to half of a right angle (π/4 rad). If we want to construct an angle of π/8 rad, we should note that π/8 rad equals exactly half of π/4 rad. Then we can construct a square, draw one of its diagonals, and bisect the angle between the diagonal and any of the sides. We'll get two adjacent angles, both of measure π/8 rad, as shown below. The correct choice is D.

This process won't work with a parallelogram, a rhombus, or a rectangle in the general case; it will only work if such a figure happens, by chance, to form a square. Therefore, choices A, B, and C are all wrong.

8. An angle of 67.5º measures 3π/8 rad. In order to construct an angle that has this measure, we can construct an angle of π/8 rad by following the procedure described in choice D of Question 7. Then we can reproduce that angle twice, each time placing the new angle adjacent to the previous one. When we've finished the process, the outermost sides of the resulting set of line segments (or, if you prefer, rays) will contain an angle of 3π/8 rad or 67.5º. The correct choice is C.

9. If you want to construct a parallelogram, you should begin by constructing two parallel lines, because in any parallelogram, pairs of opposite sides are always parallel. Once you've constructed a pair of parallel lines, you can construct a second pair of parallel lines, both of which cross both of the original parallel lines. Then, if you trace around the line segments connecting the four intersection points (making sure never to cross over your previous path), you'll have defined a parallelogram. The correct choice is C.

10. You can never "legally" use any sort of calibrated scale, either on the straight edge or the compass, in a geometric construction. Choice A constitutes a clear violation of "construction law," so it's the answer here.