| Geometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 7 |
| 1. Line N runs perpendicular to both lines L and M, which lie in, and define, plane X. (Remember that π/2 rad represents a right angle, and when two lines intersect at a right angle, they are mutually perpendicular.) Lines L, M, and N all intersect at point S. Therefore, by definition, line N constitutes a normal (or perpendicular line) to plane X at point S. The correct choice is D. |
| 2. If we remove only the outer boundary line segments of a polygon in a plane (or the outer boundary curves of any figure in a plane), our action has no effect on either the perimeter or the interior area of the object enclosed by that boundary. The definition of the perimeter doesn't depend on whether or not we consider the boundary as part of the figure that it encloses. The boundary line segments and/or curves are "infinitely thin," so the boundary itself has no area. The correct choice is A. |
| 3. If you encounter any of the expressions mentioned in this question, you should assume that the author intends to specify the shortest possible distance. The author might specify some other distance (besides the shortest distance) between points that lie on the two objects; but unless the author actually says otherwise, you should assume that she means the shortest possible distance. The correct choice is B. |
| 4. In Figure 7-20 on page 191, ∠PTR and ∠STQ are vertical angles, so we can have absolute confidence that they have equal measures. The correct answer is A. |
| 5. If two planes in Euclidean three-space share no points (they don't intersect), then they're parallel, and vice-versa. In Euclidean space, two planes must always be parallel, having no points in common, or else coincide, having all of their points in common. The answer is C. |
| 6. In order to uniquely define a plane in Euclidean three-space, we must know the locations of at least three points. In fact, three points are all that we need. Three points always define exactly one plane in Euclidean three-space. If we encounter more than three points in space, they might all lie in the same plane, but that state of affairs would constitute a great coincidence! The correct response to this question is choice B. |
|
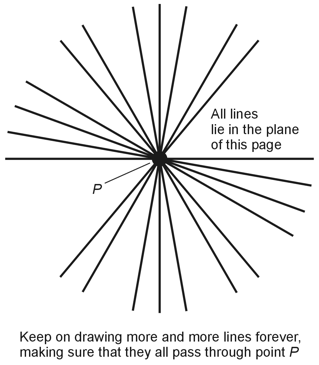
7. This question asks for the largest possible number of intersecting lines that can uniquely define a plane in Euclidean three-space. The answer: There exists no limit (there are infinitely many). A certain set of lines uniquely defines a plane if and only if they all lie in that plane. Obviously, we can keep on constructing lines in a specific plane (as defined by a sheet of paper, for example) forever. We can make sure that the lines all intersect by constructing them all through a common central point as shown in the diagram below. The correct choice is D.
|
|
8. In the situation of Figure 7-21 on page 192, the angles having measures u and v are supplementary angles, so we know that those two measures must add up to π rad or 180º (the measure of the straight angle defined by line L as it passes through point S). We can express this fact as an equation by writing u + v = π The correct choice is C. |
| 9. Two lines in space run parallel to each other if and only if they lie in the same plane and do not intersect. When two lines meet both of those criteria, then they can't possibly run askew (look back at the definition of skew lines on page 172). The correct choice is D, "All of the above." |
| 10. When we have a line in space and a point that doesn't lie on that line, we can find one and only one (in other words, exactly one) plane that contains both the line and the point. Imagine the line as a "hinge" on which we can rotate a movable plane freely. The plane will contain the external point only at one specific orientation; we must rotate the plane to "just the right place." The correct choice is A. |