| Geometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 9 |
|
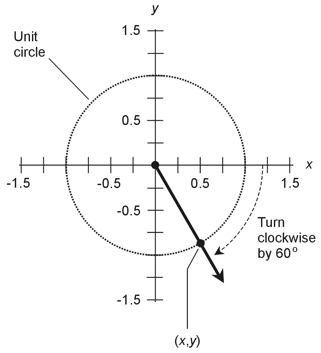
1. On a unit circle in the Cartesian xy-plane, the x-value of a point equals the cosine of the angle between the positive x axis and a ray running outward from the origin through the point on the circle in question. In this case, the ray subtends an angle of -60º with respect to the positive x axis, as shown in the drawing below.
The angle has a negative value because we must turn clockwise by 60º to get from the positive x axis to the ray. The angle would have a positive value if we had to turn counterclockwise. When we use a calculator, we find that cos -60º = 0.500 accurate to three decimal places. The correct choice is A. |
2. On a unit circle in the Cartesian plane, the y-value of a point equals the sine of the angle between the positive x axis and a ray running outward from the origin through the point on the circle in question. The drawing for the solution to Question 1 (above) shows the situation here as well. A calculator tells us that sin -60º = -0.866 accurate to three decimal places. The answer is D. |
|
3. When we want to convert an xy-plane vector with a starting point (x0,y0) and an end point (x1,y1) into standard form, we subtract the coordinates of the starting point from the coordinates of the end point. In this case, the vector starts at (x0,y0) = (3,-7) and ends at (x1,y1) = (-7,3) When we take the difference between the x-coordinates, we get x1 - x0 = -7 - 3 When we take the difference between the y-coordinates, we get y1 - y0 = 3 - (-7) Our standard-form vector is (-10,10). The correct choice is B. |
|
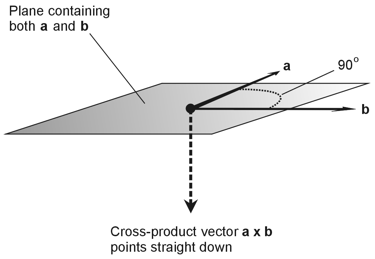
4. You can use the right-hand rule to determine the direction in which any cross-product vector points (as long as the two vectors in question don't happen to run off in the same direction, in which case the cross product equals the zero vector). In the situation of Fig. 9-14, think of the plane containing vectors a and b as horizontally oriented. In that case, the cross product a x b points straight down, as shown below.
To take advantage of the right-hand rule, extend your right arm straight out horizontally, turn your hand so that your palm faces toward your right and the little finger is on top, and then curl your fingers in a clockwise direction as viewed from above (from vector a rotating towards vector b in the drawing here). Point your thumb out, as if you want to "hitchhike." In a normal "hitchhiking" operation, you'd point your thumb upward, but in this situation, you'll see that it points straight down! The correct choice is B. |
| 5. We can calculate the dot product of two vectors by multiplying their lengths by each other, and then multiplying that result by the cosine of the angle between them. In the scenario of Fig. 9-14, the angle between vectors a and b is 90º. Using a calculator (or our memories, if we've taken any trigonometry courses), we see that cos 90º = 0. The dot product of these two vectors equals 0. Their lengths don't matter, because we always end up multiplying the product of the vector lengths by 0. The answer is A. |
| 6. Let's refer back to page 224 of the text, where Fig. 9-2 illustrates the parallelogram method of vector addition. Based on this diagram, we can envision what happens when we add the vectors in Fig. 9-14: The resultant sum vector a + b must run off in the plane containing the original two vectors a and b, and in some direction between them. The correct choice is C. |
|
7. When we want to add two vectors in the Cartesian xy-plane, we add the x-coordinates and the y-coordinates separately, and then reassemble them to get the result. In this case, we have (3,-7) + (6,2) = [(3+6),(-7+2)] The answer is A. |
|
8. To find the dot product of two vectors in the Cartesian xy-plane, we multiply the x-coordinates by each other, then multiply the y-coordinates by each other, and finally add the two products. In this case, we have (3,-7) • (6,2) = (3 x 6) +
(-7 x 2) The correct choice is B. |
|
9. These two vectors appear in Cartesian xyz-space as the ordered triples 4i + 2j - 3k = (4,2,-3) and -2i + 4j + 7k = (-2,4,7) To find the dot product, we multiply the x-coordinates (the ones with the unit vector i) by each other, then multiply the y-coordinates (the ones with the unit vector j) by each other, then multiply the z-coordinates (the ones with the unit vector k) by each other, and finally add all three products. In this situation, we get (4i + 2j - 3k) •
(-2i + 4j + 7k) = (4,2,-3) • (-2,4,7) The answer is C. |
10. We can recognize the format of this equation as that of a plane in Cartesian xyz-space. We know that the plane doesn't pass through the origin, because when we determine the x-, y-, and z-intercepts, we find that none of them lie at the origin. The correct choice is D. |