| Physics Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 3 |
| 1. By definition, impulse comprises a specific force applied for a certain length of time. Therefore, impulse equals force multiplied by time. The correct choice is A. The direction matters here, because force is a vector quantity, requiring both magnitude and direction for full expression. |
| 2. To calculate the mechanical (kinetic) energy that you must expend to lift a certain
mass by a certain distance in a gravitational field having a certain acceleration, you can
multiply the mass (in kilograms) by the distance (in meters) by the acceleration (in
meters per second squared) to get the kinetic energy Ek in joules (J),
equivalent to kilogram meters squared per second squared. In this case the mass equals
5.00 kg, the distance equals 4.00 m, and the gravitational acceleration equals 2.00 m/s2,
so Ek = 5.00 x 4.00 x 2.00 The correct choice is C. Note that the required mechanical energy equals the amount of potential energy that the object gains as a result of lifting. |
| 3. The product of mass and time, all by itself, doesn't produce a meaningful quantity in mechanics. We can calculate momentum (choice A) or impulse (choice C) if we know the rate at which the space ship accelerates, but we don't have that information, and we have no way to calculate it. We know only the fact that the acceleration is constant. Velocity (choice D) is a vector quantity representing speed and direction. The speed of our ship changes because it accelerates at a constant rate, and we lack the necessary information to calculate the velocity at any particular moment in time anyhow. The correct answer is D, "None of the above." |
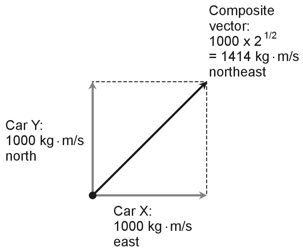
| 4. Car X, whose mass equals 1000 kg, travels at a speed of 1.000 m/s toward the east,
while car Y, whose mass also equals 1000 kg, travels at 1.000 m/s toward the north. The
two cars follow a collision course; soon they will crash! Immediately prior to the
collision, car X has a momentum vector of 1000 kg · m/s toward the east, and car Y has a
momentum vector of 1000 kg · m/s toward the north. Here's a vector diagram of the
situation. North corresponds to "straight up" and east corresponds to
"straight toward the right."
The total system momentum just before the collision equals the vector sum of the individual car momentums. We can represent that quantity as the diagonal of a square with the vectors for cars X and Y forming adjacent sides. The diagonal runs northeast, and its length equals the square root of 2 times 1000, or 1414 kg · m/s. The correct choice is B. |
| 5. To calculate the kinetic energy Ek (in joules) in a known mass
moving at a known, constant velocity, we square the velocity magnitude (in meters per
second), then multiply by the mass (in kilograms), and finally divide by 2. In
this case we have Ek = 80.00 x 5.0002 / 2.000 The correct choice is B. |
| 6. For motion in a straight line, impulse magnitude I equals force magnitude F
multiplied by time t. The force magnitude F equals the mass m
times the acceleration magnitude a. If the acceleration vector remains constant
for the entire time span t, as it does in this situation, then a = (v2 - v1) / t where a represents the acceleration magnitude, v1 represents the starting velocity magnitude, and v2 represents the final velocity magnitude. We're given information in units of meters, kilograms, and seconds, with v1 = 0.000 m/s (the boat starts out at rest), v2 = 5.000 m/s, and t = 5.000 s. Therefore a = (5.000 - 0.000) / 5.000 The boat has mass m = 4000 kg. We can calculate the constant force magnitude as F = ma Finally, the impulse magnitude comes out as I = Ft The correct choice is A. |
| 7. Power, by definition, expresses the rate at which energy manifests itself at any given instant in time. A watt, for example, equals a joule per second. The correct choice is B. |
| 8. When two objects, both traveling at constant velocity, collide and "stick" to each other, the total momentum after the collision equals the total momentum before the collision. Momentum is conserved; that's "the law"! The correct choice is C. |
| 9. If we attempt to make a calculation among quantities whose units aren't compatible, we can't directly multiply or divide the units by each other. For example, if we want to calculate the momentum vector magnitude for a 100-kg object traveling at a constant straight-line speed of 15 mi/h, we can't multiply 100 by 15 and expect to get an answer in sensible units! We must first convert the speed from miles per hour to meters per second. Then we can do the arithmetic and get a meaningful answer in kilogram-meters per second. The answer is D. |
| 10. If we encounter a quantity in gram-centimeters per second, we can convert grams to kilograms, and convert centimeters to meters. Then we have kilogram-meters per second, and we can recognize that unit combination as an expression of momentum. The correct choice is D. |