| Trigonometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 11 |
| 1. As you read through this solution, follow along in Fig. 11-6. If you stand along
the mirror axis at a distance ro from the center of the mirror, where ro
significantly exceeds the focal length f, then the distance ri of
your body's real image from the mirror relates approximately to ro and f
according to the equation 1 / f = 1 / ri + 1 / ro In this case, f = 1.50 meters (m) and ro = 8.35 m. Therefore 1 / 1.50 = 1 / ri + 1 / 8.35 Working out the reciprocals to six significant figures to avoid cumulative rounding errors, you get 0.666667 = 1 / ri + 0.119760 You can subtract 0.119760 from both sides to obtain 0.546907 = 1 / ri Taking the reciprocals of both sides tells you that 1.82846 = ri Rounding to three significant figures produces the final answer of ri = 1.83 m. That's how far the real image lies from the center of the mirror. The correct choice is C. |
| 2. As you read through this solution, follow along in Fig. 11-9. In this situation,
you've been told that the upper medium has a refractive index of 1.05. That's r
according to the geometry here, so you know that r = 1.05 The lower medium has a refractive index of 1.75, which corresponds to s in the geometry here, so you know that s = 1.75 The ray R strikes the boundary at an incidence angle of 60º with respect to a line normal to the boundary at the "strike point." That's θ according to the geometry here, so you know that θ = 60º Now you can invoke the formula for Snell's law, which tells you that sin φ / sin θ = r / s where φ represents the angle, relative to the normal, at which ray S emerges into the lower medium. When you substitute the known values into the formula, you get sin φ / sin 60º = 1.05 / 1.75 Simplifying, and going to six significant figures, you get sin φ / 0.866025 = 0.600000 When you multiply each side by 0.866025, you obtain sin φ = 0.519615 You can take the Arcsine of both sides to get Arcsin (sin φ) = Arcsin 0.519615 which works out to φ = 31.3064º The choices all appear rounded off to the nearest degree; the correct one is B, which tells you that φ = 31º. |
| 3. In order to work this problem out, we can do either of two things. First, we can
input the angle 90º for θ and re-work the problem through just as we did when
we solved Question 2. Alternatively, we can calculate the critical angle that we'd observe
if we sent the light beam upward from underneath along the path of ray S, letting
it emerge above the boundary along the path of ray R. Let's use the first scheme,
because this question describes a ray going down (not up) through the boundary. We start
once more with the Snell's law formula sin φ / sin θ = r / s When we substitute the known values into the formula, we get sin φ / sin 90º = 1.05 / 1.75 which simplifies to sin φ / 1 = 0.600000 so therefore sin φ = 0.6000000 When we take the Arcsine of both sides, we obtain Arcsin (sin φ) = Arcsin 0.600000 which works out to φ = 36.8699º When we round off to the nearest degree, we get φ = 37º The correct choice is C. |
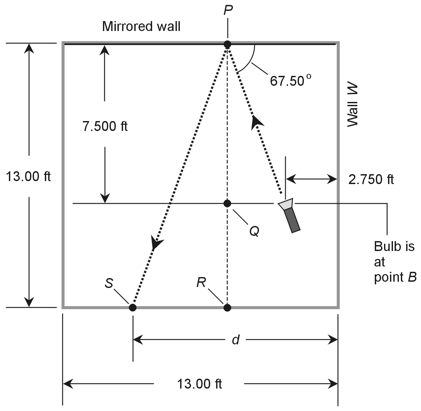
| 4. Refer to the illustration below, which is the same as Fig. 11-15 except that five
specific points have been named. Let's begin by finding out the distance of the light beam
from wall W when it hits the mirror. We can do this by examining a right triangle
connecting the flashlight bulb (point B), point P, and point Q.
In this right triangle:
Let's calculate the base length BQ. We can determine the angle of incidence at point P by subtracting 67.50º from 90º, getting 22.50º. That's the angle between the incident beam and line segment PQ. The tangent of this angle must equal BQ divided by PQ, so we have tan 22.50º = BQ / 7.500 which solves to BQ = 3.10660 ft Now we know that point Q lies 2.750 ft plus 3.10660 ft, or 5.85660 ft, from the wall. (Once again, we go to some extra significant figures to avoid cumulative rounding errors.) That's the same as the distance of the light beam from wall W when it hits the mirror at point P. It's also the distance of point R from wall W as shown in the above diagram. Now let's think about the right triangle connecting point P, point R, and point S where the light beam hits the wall opposite the mirror. In this right triangle:
Let's keep in mind the fact that when the line beam strikes the mirrored wall, the angle of reflection equals the angle of incidence, which we know is 22.50º. Based on this knowledge, we can calculate the base length RS using the equation tan 22.50º = RS / 13.00 which solves to RS = 5.38478 ft Point S must lie at a distance d from wall W equal to the sum of RS (which we've determined to equal 5.38478 ft) and the distance of point R from wall W (which we've found to be 5.85660 ft). That sum equals 11.24138 ft, which rounds to d = 11.24 ft. The correct choice is A. |
| 5. Even though the solution to the previous problem involved a lot of calculation, the entire process depended on the law of reflection, which states that when a light beam strikes a flat reflective surface, the angle of incidence equals the angle of reflection. The answer is D. |
| 6. Total internal reflection can occur when, but only when, a light ray encounters a well-defined boundary between a medium having a relatively higher index of refraction and a medium having a relatively lower index of refraction. According to Table 11-1, fresh liquid water has a refractive index of 1.33, and crown glass has a refractive index of 1.52. If a ray of light travels through fresh liquid water and strikes the surface of a sample of crown glass, total internal reflection can't occur regardless of the angle of incidence, because the second medium's refractive index exceeds the first medium's refractive index. The correct choice is D. |
| 7. In this situation, the light beam travels in the opposite direction compared with
the scenario of Question 6, so we'll see total internal reflection if the incidence angle
gets large enough. The critical angle θc is the largest angle that
an incident ray can subtend, relative to the normal, without reflecting internally at a
boundary where it encounters a medium having a relatively lower index of refraction. We
can calculate this angle as θc = Arcsin (s/r) where s represents the smaller (second medium's) index of refraction and r represents the larger (first medium's) index of refraction. In this case s = 1.33 and r = 1.52, so θc = Arcsin (1.33 / 1.52) accurate to three significant figures. The correct choice is C. |
| 8. Let's use the formula for the critical angle and input the known values. Then we
can solve for the smallest refractive index that the prism in Fig. 11-16 can have, in
order to ensure total internal reflection at its base, and assuming that the ray travels
along the path shown in the figure. The rules of geometry tell us that, as the ray
encounters the base of the prism from inside, the angle of incidence equals exactly 45º.
We want that to equal the critical angle, so we set θc = 45.0000º accurate to six significant figures. For total internal reflection to be possible, the prism must have a higher index of refraction than the surrounding medium. In this case, the surrounding medium is air with a refractive index of 1.00000. Therefore, we set s = 1.00000 The critical angle formula tells us that 45.0000º = Arcsin (1.00000 / r) where r represents the smallest index of refraction that the prism can have if we expect total internal reflection to take place at a 45.0000º incidence angle. When we take the sine of both sides, we get sin 45.0000º = sin [Arcsin (1.00000 / r)] which simplifies to 0.707107 = 1.00000 / r and solves to r = 1.414 rounded off to four significant figures. The correct choice is B. |
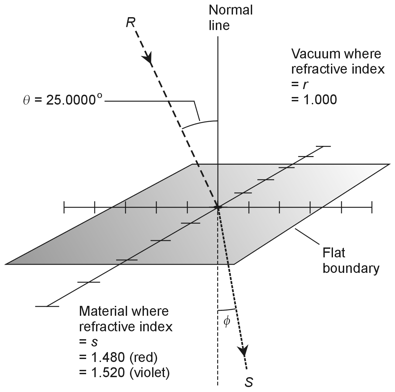
| 9. Let's envision the situation as shown in the diagram below. We represent the
incident ray, traveling through a vacuum, as R. We represent the emerging ray,
traveling in the clear solid material, as S. We assign the indices of refraction
as shown. We also set the angle of incidence to θ = 25.0000º. We want to
find the angle φ for red light, and then for violet light. The divergence angle
will equal the difference between the angles of refraction.
For the ray of red light, we have s = 1.480, so the Snell's law formula tells us that sin φ / sin θ = r / s Inputting the known values, we get sin φ / sin 25.0000º = 1.000 / 1.480 which simplifies to sin φ / 0.422618 = 0.675676 Multiplying each side by 0.422618, we get sin φ = 0.285553 We take the Arcsine of both sides and use a calculator to find that φ = 16.5919º Let's leave in the extra decimal places until the very end of the calculation process, so as to avoid cumulative rounding errors. We've just found the angle of refraction for the red ray. Now let's repeat all of the arithmetic for the violet ray, where s = 1.520. We can go through the same calculation process as we did with the red ray, but using the new values. Step-by-step, it comes out as sin φ / sin 25.0000º = 1.000 / 1.520 sin φ / 0.422618 = 0.657895 sin φ = 0.278038 φ = 16.1431º The divergence angle between the red and violet refracted rays equals the difference between the red angle of refraction and the violet angle of refraction. That's 16.5919º - 16.1431º, which works out to 0.45º when we round off to the nearest hundredth of a degree. The correct choice is B. |
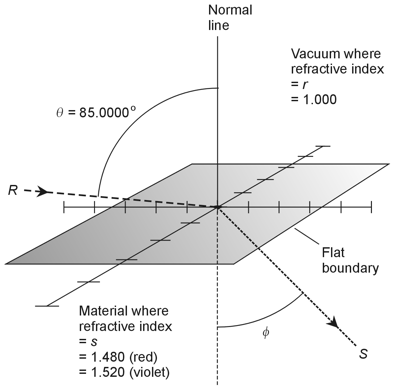
| 10. Let's revise the foregoing diagram to show the new situation (below). As before,
we represent the incident ray, traveling through a vacuum, as R. We represent the
emerging ray, traveling in the clear solid material, as S. The refractive indices
remain the same, but the angle of incidence has increased to θ = 85.0000º.
Once again, we want to find the angle φ for red light, and then for violet
light, and then find the difference between them.
Following the same process as we did when we solved the previous problem, we set s = 1.480 for the red ray and work through the calculation with the new values: sin φ / sin 85.0000º = 1.000 / 1.480 sin φ / 0.996195 = 0.675676 sin φ = 0.673105 φ = 42.3072º Now for the violet ray, for which s = 1.520: sin φ / sin 85.0000º = 1.000 / 1.520 sin φ / 0.996195 = 0.657895 sin φ = 0.655392 φ = 40.9494º In this scenario, the divergence angle between the red and violet refracted rays equals 42.3072º - 40.9494º, which works out to 1.36º when we round off to the nearest hundredth of a degree. The correct choice is D. |