| Trigonometry Demystified, 2nd edition |
| Stan Gibilisco |
| Explanations for Quiz Answers in Chapter 12 |
| 1. In the spherical triangle of Fig. 12-10, the two vertices on the equator both have
interior right angles, because they're points at which a meridian crosses the equator. (On
the earth's surface, all meridians cross the equator at right angles.) Right angles, by
definition, always measure π/2 rad. The interior angle at the north pole measures 67.5º,
which equals 3/16 of a full circle. When we convert that value to radians, we get 67.5º = 3/16 x 2π When we add up the measures of the three interior angles in radians, we obtain a sum of π/2 + π/2 + 3π/8 The correct choice is C. |
| 2. The chapter text gives us a formula for calculating the distance dlon-deg
(in kilometers) between any two meridians separated by exactly one degree of longitude, as
measured along any particular parallel at latitude θ on the earth's surface.
That formula is dlon-deg = 111.2 cos θ In this case, we're told to work at 30.00º north latitude, so θ = 30.00º. Therefore dlon-deg = 111.2 cos 30.00º Our meridians are 5.00º apart, so we must multiply the above number by 5.00. When we carry out that arithmetic and round off to the nearest kilometer, we get a distance of 482 kilometers as measured along the parallel corresponding to 30º north latitude. The correct choice is C. |
| 3. This situation resembles the one described in Question 2, except that now we have θ
= 60.00º, so the distance between two meridians one degree apart works out as dlon-deg = 111.2 cos 60.00º Multiplying by 5.00, and rounding off to the nearest kilometer, we get a distance of 278 kilometers as measured along the parallel corresponding to 60º north latitude. The answer is A. |
| 4. We can use the spherical law of sines to solve this problem. We've been told that
the three sides of a spherical triangle have angular extents of q = 30º r = 25º s = 20º Let's name the interior angles as follows:
The spherical law of sines tells us that (sin q) / (sin ψq) = (sin r) / (sin ψr) = (sin s) / (sin ψs) The problem states that the angle opposite side q, which we call ψq, constitutes a right angle, so we have the additional known value ψq = 90º Now we can put all of our known values into the formula for the spherical law of sines, getting (sin 30º) / (sin 90º) = (sin 25º) / (sin ψr) = (sin 20º) / (sin ψs) Working out to four significant figures, a calculator can simplify the formula to 0.5000 / 1.000 = 0.4226 / (sin ψr) = 0.3420 / (sin ψs) Leaving out the last third of the formula and simplifying the first third, we get 0.5000 = 0.4226 / (sin ψr) A little algebra yields the equation sin ψr = 0.8452 When we take the Arcsine of both sides, we get Arcsin (sin ψr) = Arcsin 0.8452 which solves to ψr = 58º rounded off to the nearest degree. The correct choice is C. |
| 5. We keep the same scenario as we had in Question 4 and its solution, but now we want
to know the measure of ψs, the angle opposite side s. Let's go
back to the general formula that we got in the middle of our solution to Question 4, which
told us that 0.5000 / 1.000 = 0.4226 / (sin ψr) = 0.3420 / (sin ψs) Leaving out the middle third of the formula and simplifying the first third, we get 0.5000 = 0.3420 / (sin ψs) which simplifies to sin ψs = 0.6840 When we take the Arcsine of both sides, we get Arcsin (sin ψs) = Arcsin 0.6840 which solves to ψs = 43º rounded off to the nearest degree. The answer is D. |
| 6. We've found the measures of all three interior angles of the spherical triangle
described in Question 4. Those measures are ψq = 90º ψr = 58º ψs = 43º They add up to 191º. The answer is B. |
| 7. Each and every individual meridian intersects the equator at a right angle, or π/2 rad. That would of course include the meridian corresponding to 45º east longitude. The correct choice is B. |
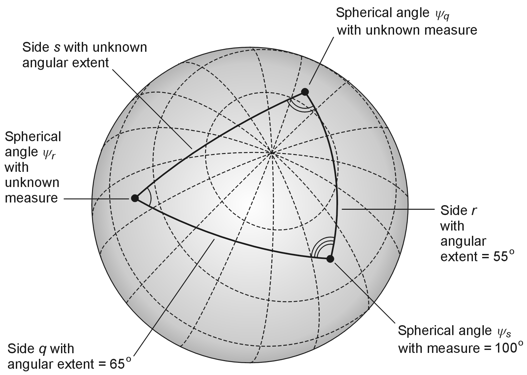
| 8. We need the spherical law of cosines to solve this problem. If we know the angular
extents of two of the sides, say q and r, of a spherical triangle, and we
also know the measure of the spherical angle ψs between those two
sides, then we can calculate the cosine of the angular extent of the third side s
as cos s = cos q cos r + sin q sin r cos ψs In the situation of Fig. 12-11, let's use the following names for the sides of the spherical triangle and their angular extents: q = 65º r = 55º s = (unknown) Let's name the interior angles this way:
The diagram below is an enhanced version of Fig. 12-11 with these labels included.
When we plug in the known values to the formula for the spherical law of cosines, we get cos s = cos 65º cos 55º + sin 65º sin 55º cos 100º When we work out the sines and cosines to four significant figures (a few more than we'll need, to ensure that we don't suffer with cumulative rounding errors), we get cos s = 0.4226 x 0.5736 + 0.9063 x 0.8192 x (-0.1736) Taking the Arccosine of both sides, and rounding off the result to the nearest degree, we get Arccos (cos s) = Arccos 0.1135 which tells us that s = 83º. The correct choice is A. |
| 9. We can use the spherical law of sines to solve this problem. Once again, the
formula is (sin q) / (sin ψq) = (sin r) / (sin ψr) = (sin s) / (sin ψs) We want to find the measure of the interior angle at the far-left vertex. That's angle ψr. We found the angular extent of side s (see the drawing above) when we worked out the solution to Question 8. We can therefore set up the ratio equality (sin r) / (sin ψr) = (sin s) / (sin ψs) and plug in the known values to get (sin 55º) / (sin ψr) = (sin 83º) / (sin 100º) which calculates out to 0.8192 / (sin ψr) = 0.9925 / 0.9848 and simplifies to sin ψr = 0.8128 When we take the Arcsine of both sides and round off the result to the nearest degree, we obtain Arcsin (sin ψr) = Arcsin 0.8128 so ψr = 54º. The answer is A. |
| 10. We can use the spherical law of sines to solve this problem, along similar lines to
the previous solution. Once again, we start with the original formula for the law of sines:
(sin q) / (sin ψq) = (sin r) / (sin ψr) = (sin s) / (sin ψs) We want to find the measure of the interior angle at the top-right vertex. That's angle ψq. We found the angular extent of side s (see the drawing above) when we worked out the solution to Question 8. We can therefore set up the ratio equality (sin q) / (sin ψq) = (sin s) / (sin ψs) and plug in the known values to get (sin 65º) / (sin ψq) = (sin 83º) / (sin 100º) which calculates out to 0.9063 / (sin ψq) = 0.9925 / 0.9848 and simplifies to sin ψq = 0.8993 When we take the Arcsine of both sides and round off the result to the nearest degree, we have Arcsin (sin ψq) = Arcsin 0.8993 so ψq = 64º. The answer is B. |